Бісектриса трикутника: визначення, властивості та формули
Хто з нас не креслив у зошиті трикутники на уроках геометрії? Часом ці лінії та кути здавались просто значками на папері. Але коли ми бачимо, як архітектор проектує дах будинку чи інженер створює міст, ми розуміємо справжню силу геометрії. І бісектриса трикутника – одна з тих ліній, яка має дивовижні властивості та практичне значення.
Що таке бісектриса трикутника?
Бісектриса трикутника – це відрізок, який сполучає вершину трикутника з точкою на протилежній стороні та ділить кут при цій вершині навпіл. Коли ми говоримо про бісектрису, ми маємо на увазі саме цей відрізок від вершини до протилежної сторони, а не промінь, що йде в нескінченність.
У кожному трикутнику є три бісектриси – по одній з кожної вершини. Вони завжди перетинаються в одній точці, яку називають інцентром. Ця точка – центр вписаного кола трикутника.
Головні властивості бісектриси
Бісектриси мають кілька важливих властивостей, які допомагають розв’язувати геометричні задачі:
- Бісектриса ділить протилежну сторону трикутника на відрізки, пропорційні прилеглим сторонам. Якщо AD – бісектриса трикутника ABC, то виконується співвідношення: AB/AC = BD/DC. Це основна теорема бісектриси.
- Всі три бісектриси трикутника перетинаються в одній точці – інцентрі трикутника.
- Інцентр – це центр вписаного кола трикутника, яке дотикається до всіх трьох сторін.
- У рівнобедреному трикутнику бісектриса, проведена з вершини до основи, є також висотою та медіаною.
- У рівносторонньому трикутнику всі три бісектриси рівні між собою.
 Як обчислити довжину бісектриси
Як обчислити довжину бісектриси
Щоб знайти довжину бісектриси в трикутнику, ми можемо використати формулу:
La = 2bc·cos(α/2) / (b+c)
де:
- La – довжина бісектриси з вершини A
- b і c – довжини сторін, прилеглих до вершини A
- α – кут при вершині A
Наприклад, якщо в трикутнику сторони b = 6 см, c = 8 см і кут α = 60°, то довжина бісектриси буде: La = 2·6·8·cos(30°) / (6+8) = 96·0,866 / 14 = 5,94 см
Приклад задачі з бісектрисою
 Розглянемо практичну задачу: в трикутнику ABC відомі сторони AB = 5 см, AC = 7 см і бісектриса AD = 4 см. Потрібно знайти довжину сторони BC.
Розглянемо практичну задачу: в трикутнику ABC відомі сторони AB = 5 см, AC = 7 см і бісектриса AD = 4 см. Потрібно знайти довжину сторони BC.
Розв’язання:
- За теоремою бісектриси: AB/AC = BD/DC
- Підставимо відомі значення: 5/7 = BD/DC
- Позначимо DC = x, тоді BD = BC – x
- З пропорції: 5/7 = (BC – x)/x
- 5x = 7(BC – x)
- 5x = 7BC – 7x
- 12x = 7BC
- x = 7BC/12
Використовуючи формулу для довжини бісектриси та підставляючи знайдене значення x, можемо обчислити BC. Звичайно, розв’язання повне вимагає додаткових кроків, але це демонструє, як властивості бісектриси допомагають у розв’язанні задач.
Практичне застосування бісектрис
Бісектриси знаходять застосування не лише в теоретичній геометрії:
- Архітектори використовують властивості бісектрис при проектуванні симетричних елементів будівель.
- Інженери застосовують їх для розрахунку рівномірного розподілу навантаження в конструкціях.
- У навігації та картографії бісектриси допомагають визначати оптимальні шляхи та відстані.
Коли ми дивимось на парк з красивими алеями, що розходяться від центральної площі, ми часто бачимо принцип бісектрис у дії – вони створюють рівномірний розподіл простору.
Бісектриса трикутника – це не просто лінія на папері. Це потужний інструмент у геометрії, який має чіткі властивості та широке застосування. Розуміння бісектрис допомагає нам бачити світ через призму математичної гармонії та використовувати ці знання для розв’язання практичних задач.
Спробуйте знайти приклади бісектрис у повсякденному житті – від дизайну логотипів до архітектури будівель. Ви здивуєтесь, наскільки часто ця проста геометрична концепція зустрічається навколо нас.

Пишу про все, що надихає та змушує задуматися. Маю журналістську освіту та багато років досвіду у створенні пізнавальних матеріалів. Захоплююсь наукою, культурою та історіями успіху. Шукаю цікаве в усьому, аби ділитися знаннями, які допомагають відкривати нові горизонти, бачити красу світу та отримувати корисні поради для життя.

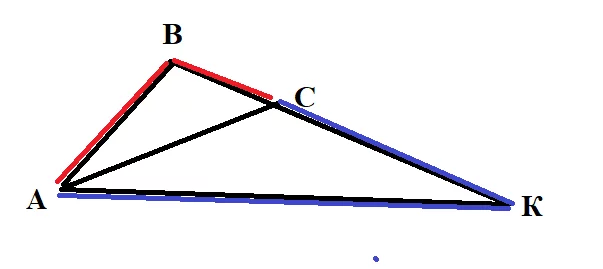 Як обчислити довжину бісектриси
Як обчислити довжину бісектриси